Chapter 14: Mathematical Foundations
Contents
Software professionals live with programs. In a very simple language, one can program only for something that follows a well-understood, nonambiguous logic. The Mathematical Foundations knowledge area (KA) helps software engineers comprehend this logic, which in turn is translated into programming language code. The mathematics that is the primary focus in this KA is quite different from typical arithmetic, where numbers are dealt with and discussed. Logic and reasoning are the essence of mathematics that a software engineer must address.
Mathematics, in a sense, is the study of formal systems. The word “formal” is associated with preciseness, so there cannot be any ambiguous or erroneous interpretation of the fact. Mathematics is therefore the study of any and all certain truths about any concept. This concept can be about numbers as well as about symbols, images, sounds, video—almost anything. In short, not only numbers and numeric equations are subject to preciseness. On the contrary, a software engineer needs to have a precise abstraction on a diverse application domain.
The SWEBOK Guide’s Mathematical Foundations KA covers basic techniques to identify a set of rules for reasoning in the context of the system under study. Anything that one can deduce following these rules is an absolute certainty within the context of that system. In this KA, techniques that can represent and take forward the reasoning and judgment of a software engineer in a precise (and therefore mathematical) manner are defined and discussed. The language and methods of logic that are discussed here allow us to describe mathematical proofs to infer conclusively the absolute truth of certain concepts beyond the numbers. In short, you can write a program for a problem only if it follows some logic. The objective of this KA is to help you develop the skill to identify and describe such logic. The emphasis is on helping you understand the basic concepts rather than on challenging your arithmetic abilities.
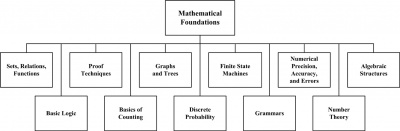
The breakdown of topics for the Mathematical Foundations KA is shown in Figure 14.1.
1 Set, Relations, Functions
Set. A set is a collection of objects, called elements of the set. A set can be represented by listing its elements between braces, e.g., S = {1, 2, 3}.
The symbol ∈ is used to express that an element belongs to a set, or—in other words—is a member of the set. Its negation is represented by ∉, e.g., 1 ∈ S, but 4 ∉ S.
In a more compact representation of set using set builder notation, {x | P(x)} is the set of all x such that P(x) for any proposition P(x) over any universe of discourse. Examples for some important sets include the following:
- N = {0, 1, 2, 3, …} = the set of nonnegative integers.
- Z = {…, −3, −2, −1, 0, 1, 2, 3, …} = the set of integers.
Finite and Infinite Set. A set with a finite number of elements is called a finite set. Conversely, any set that does not have a finite number of elements in it is an infinite set. The set of all natural numbers, for example, is an infinite set.
Cardinality. The cardinality of a finite set S is the number of elements in S. This is represented |S|, e.g., if S = {1, 2, 3}, then |S| = 3.
Universal Set. In general S = {x ∈ U | p(x)}, where U is the universe of discourse in which the predicate P(x) must be interpreted. The “universe of discourse” for a given predicate is often referred to as the universal set. Alternately, one may define universal set as the set of all elements.
Set Equality. Two sets are equal if and only if they have the same elements, i.e.:
- X = Y ≡ ∀p (p ∈ X ↔ p ∈ Y).
Subset. X is a subset of set Y, or X is contained in Y, if all elements of X are included in Y. This is denoted by X ⊆ Y. In other words, X ⊆ Y if and only if ∀p (p ∈ X → p ∈ Y). For example, if X = {1, 2, 3} and Y = {1, 2, 3,4, 5}, then X ⊆ Y. If X is not a subset of Y, it is denoted as X ⊈ Y.
Proper Subset. X is a proper subset of Y (denoted by X ⊂ Y) if X is a subset of Y but not equal to Y, i.e., there is some element in Y that is not in X. In other words, X ⊂ Y if (X ⊆ Y) ∧ (X ≠ Y). For example, if X = {1, 2, 3}, Y = {1, 2, 3, 4}, and Z = {1, 2, 3}, then X ⊂ Y, but X is not a proper subset of Z. Sets X and Z are equal sets. If X is not a proper subset of Y, it is denoted as X ⊄ Y.
Superset. If X is a subset of Y, then Y is called a superset of X. This is denoted by Y ⊇ X, i.e., Y ⊇ X if and only if X ⊆ Y. For example, if X = {1, 2, 3} and Y = {1, 2, 3,4, 5}, then Y ⊇ X.
Empty Set. A set with no elements is called an empty set. An empty set, denoted by ∅, is also referred to as a null or void set.
Power Set. The set of all subsets of a set X is called the power set of X. It is represented as ℘(X). For example, if X = {a, b, c}, then ℘(X) = {∅,{a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}}. If |X| = n, then |℘(X)| = 2n.
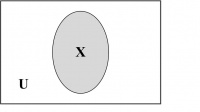
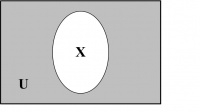
Venn Diagrams. Venn diagrams are graphic representations of sets as enclosed areas in the plane. For example, in Figure 14.2, the rectangle represents the universal set and the shaded region represents a set X.
1.1 Set Operations
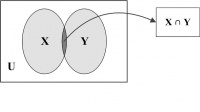
Intersection. The intersection of two sets X and Y, denoted by X ∩ Y, is the set of common elements in both X and Y. In other words, X ∩ Y = {p | (p ∈ X) ∧ (p ∈ Y)}. As, for example, {1, 2, 3} ∩ {3, 4, 6} = {3}. If X ∩ Y = f, then the two sets X and Y are said to be a disjoint pair of sets.
A Venn diagram for set intersection is shown in Figure 14.3. The common portion of the two sets represents the set intersection.
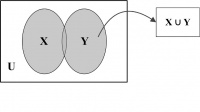
Union. The union of two sets X and Y, denoted by X ∪ Y, is the set of all elements either in X, or in Y, or in both. In other words, X ∪ Y = {p | (p ∈ X) ∨ (p ∈ Y)}. As, for example, {1, 2, 3} ∪ {3, 4, 6} = {1, 2, 3, 4, 6}. It may be noted that |X ∪ Y| = |X| + |Y| − |X ∩ Y|.
A Venn diagram illustrating the union of two sets is represented by the shaded region in Figure 14.4.
Complement. The set of elements in the universal set that do not belong to a given set X is called its complement set X'. In other words, X' ={p | (p ∈ U) ∧ (p ∉ X)}. The shaded portion of the Venn diagram in Figure 14.5 represents the complement set of X
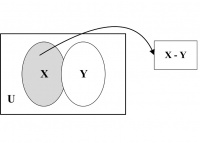
Set Difference or Relative Complement. The set of elements that belong to set X but not to set Y builds the set difference of Y from X. This is represented by X − Y. In other words, X − Y = {p | (p ∈ X) ∧ (p ∉ Y)}. As, for example, {1, 2, 3} − {3, 4, 6} = {1, 2}. It may be proved that X − Y = X ∩ Y’. Set difference X – Y is illustrated by the shaded region in Figure 14.6 using a Venn diagram.
Cartesian Product. An ordinary pair {p, q} is a set with two elements. In a set, the order of the elements is irrelevant, so {p, q} = {q, p}. In an ordered pair (p, q), the order of occurrences of the elements is relevant. Thus, (p, q) ≠ (q, p) unless p = q. In general (p, q) = (s, t) if and only if p = s and q = t. Given two sets X and Y, their Cartesian product X × Y is the set of all ordered pairs (p, q) such that p ∈ X and q ∈ Y. In other words, X × Y = {(p, q) | (p ∈ X) ∧ (q ∈ Y)}. As for example, {a, b} × {1, 2} = {(a, 1), (a, 2), (b, 1), (b, 2)}
1.2 Properties of Set
Some of the important properties and laws of sets are mentioned below.
1. Associative Laws:
X ∪ (Y ∪ Z) = (X ∪ Y) ∪ Z
X ∩ (Y ∩ Z) = (X ∩ Y) ∩ Z
2. Commutative Laws:
X ∪ Y = Y ∪ X
X ∩ Y = Y ∩ X
3. Distributive Laws:
X ∪ (Y ∩ Z) = (X ∪ Y) ∩ (X ∪ Z)
X ∩ (Y ∪ Z) = (X ∩ Y) ∪ (X ∩ Z)
4. Identity Laws:
X ∪ ∅ = X
X ∩ U = X
5. Complement Laws:
X ∪ X' = U
X ∩ X' = ∅
6. Idempotent Laws:
X ∪ X = X
X ∩ X = X
7.Bound Laws:
X ∪ U = U
X ∩ ∅ = ∅
8. Absorption Laws:
X ∪ (X ∩ Y) = X
X ∩ (X ∪ Y) = X
9. De Morgan’s Laws:
(X ∪ Y)' = X' ∩ Y'
(X ∩ Y)' = X' ∪ Y'
1.3 Relation and Function
A relation is an association between two sets of information. For example, let’s consider a set of residents of a city and their phone numbers. The pairing of names with corresponding phone numbers is a relation. This pairing is ordered for the entire relation. In the example being considered, for each pair, either the name comes first followed by the phone number or the reverse. The set from which the first element is drawn is called the domain set and the other set is called the range set. The domain is what you start with and the range is what you end up with.
A function is a well-behaved relation. A relation R(X, Y) is well behaved if the function maps every element of the domain set X to a single element of the range set Y. Let’s consider domain set X as a set of persons and let range set Y store their phone numbers. Assuming that a person may have more than one phone number, the relation being considered is not a function. However, if we draw a relation between names of residents and their date of births with the name set as domain, then this becomes a well-behaved relation and hence a function. This means that, while all functions are relations, not all relations are functions. In case of a function given an x, one gets one and exactly one y for each ordered pair (x, y).
For example, let’s consider the following two relations.
- A: {(3, –9), (5, 8), (7, –6), (3, 9), (6, 3)}.
- B: {(5, 8), (7, 8), (3, 8), (6, 8)}.
Are these functions as well? In case of relation A, the domain is all the x-values, i.e., {3, 5, 6, 7}, and the range is all the y-values, i.e., {–9, –6, 3, 8, 9}. Relation A is not a function, as there are two different range values, –9 and 9, for the same x-value of 3. In case of relation B, the domain is same as that for A, i.e., {3, 5, 6, 7}. However, the range is a single element {8}. This qualifies as an example of a function even if all the x-values are mapped to the same y-value. Here, each x-value is distinct and hence the function is well behaved. Relation B may be represented by the equation y = 8.
The characteristic of a function may be verified using a vertical line test, which is stated below:
Given the graph of a relation, if one can draw a vertical line that crosses the graph in more than one place, then the relation is not a function.
In this example, both lines L1 and L2 cut the graph for the relation thrice. This signifies that for the same x-value, there are three different y-values for each of case. Thus, the relation is not a function
2 Basic Logic
2.1 Propositional Logic
A proposition is a statement that is either true or false, but not both. Let’s consider declarative sentences for which it is meaningful to assign either of the two status values: true or false. Some examples of propositions are given below.
- 1. The sun is a star
- 2. Elephants are mammals.
- 3. 2 + 3 = 5.
However, a + 3 = b is not a proposition, as it is neither true nor false. It depends on the values of the variables a and b.
The Law of Excluded Middle: For every proposition p, either p is true or p is false.
The Law of Contradiction: For every proposition p, it is not the case that p is both true and false.
Propositional logic is the area of logic that deals with propositions. A truth table displays the relationships between the truth values of propositions.
A Boolean variable is one whose value is either true or false. Computer bit operations correspond to logical operations of Boolean variables.
The basic logical operators including negation (¬ p), conjunction (p ∧ q), disjunction (p ∨ q), exclusive or (p ⊕ q), and implication (p → q) are to be studied. Compound propositions may be formed using various logical operators.
A compound proposition that is always true is a tautology. A compound proposition that is always false is a contradiction. A compound proposition that is neither a tautology nor a contradiction is a contingency.
Compound propositions that always have the same truth value are called logically equivalent (denoted by ≡). Some of the common equivalences are:
Identity laws:
p ∧ T ≡ p
p ∨ F ≡ p
Domination laws:
p ∨ T ≡ T
p ∧ F ≡ F
Idempotent laws:
p ∨ p ≡ p
p ∧ p ≡ p
Double negation law:
¬ (¬ p) ≡ p
Commutative laws:
p ∨ q ≡ q ∨ p
p ∧ q ≡ q ∧ p
Associative laws:
(p ∨ q) ∨ r ≡ p ∨ (q ∨ r)
(p ∧ q) ∧ r ≡ p ∧ (q ∧ r)
Distributive laws:
p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r)
p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)
De Morgan’s laws:
¬ (p ∧ q) ≡ ¬ p ∨ ¬ q
¬ (p ∨ q) ≡ ¬ p ∧ ¬ q
2.2 Predicate Logic
A predicate is a verb phrase template that describes a property of objects or a relationship among objects represented by the variables. For example, in the sentence, The flower is red, the template is red is a predicate. It describes the property of a flower. The same predicate may be used in other sentences too.
Predicates are often given a name, e.g., “Red” or simply “R” can be used to represent the predicate is red. Assuming R as the name for the predicate is red, sentences that assert an object is of the color red can be represented as R(x), where x represents an arbitrary object. R(x) reads as x is red
Quantifiers allow statements about entire collections of objects rather than having to enumerate the objects by name.
The Universal quantifier ∀x asserts that a sentence is true for all values of variable x. For example, ∀x Tiger(x) → Mammal(x) means all tigers are mammals.
The Existential quantifier ∃x asserts that a sentence is true for at least one value of variable x. For example, ∃x Tiger(x) → Man-eater(x) means there exists at least one tiger that is a man-eater.
Thus, while universal quantification uses implication, the existential quantification naturally uses conjunction.
A variable x that is introduced into a logical expression by a quantifier is bound to the closest enclosing quantifier. A variable is said to be a free variable if it is not bound to a quantifier.
Similarly, in a block-structured programming language, a variable in a logical expression refers to the closest quantifier within whose scope it appears.
For example, in ∃x (Cat(x) ∧ ∀x (Black(x))), x in Black(x) is universally quantified. The expression implies that cats exist and everything is black.
Propositional logic falls short in representing many assertions that are used in computer science and mathematics. It also fails to compare equivalence and some other types of relationship between propositions.
For example, the assertion a is greater than 1 is not a proposition because one cannot infer whether it is true or false without knowing the value of a. Thus, propositional logic cannot deal with such sentences. However, such assertions appear quite often in mathematics and we want to infer on those assertions. Also, the pattern involved in the following two logical equivalences cannot be captured by propositional logic: “Not all men are smokers” and “Some men don’t smoke.” Each of these two propositions is treated independently in propositional logic. There is no mechanism in propositional logic to find out whether or not the two are equivalent to one another. Hence, in propositional logic, each equivalent proposition is treated individually rather than dealing with a general formula that covers all equivalences collectively.
Predicate logic is supposed to be a more powerful logic that addresses these issues. In a sense, predicate logic (also known as first-order logic or predicate calculus) is an extension of propositional logic to formulas involving terms and predicates.
3 Proof Techniques
A proof is an argument that rigorously establishes the truth of a statement. Proofs can themselves be represented formally as discrete structures.
Statements used in a proof include axioms and postulates that are essentially the underlying assumptions about mathematical structures, the hypotheses of the theorem to be proved, and previously proved theorems.
A theorem is a statement that can be shown to be true.
A lemma is a simple theorem used in the proof of other theorems.
A corollary is a proposition that can be established directly from a theorem that has been proved.
A conjecture is a statement whose truth value is unknown.
When a conjecture’s proof is found, the conjecture becomes a theorem. Many times conjectures are shown to be false and, hence, are not theorems.
3.1 Methods of Proving Theorems
Direct Proof. Direct proof is a technique to establish that the implication p → q is true by showing that q must be true when p is true.
For example, to show that if n is odd then n2−1 is even, suppose n is odd, i.e., n = 2k + 1 for some integer k: ∴ n2 = (2k + 1)2 = 4k2 + 4k + 1
As the first two terms of the Right Hand Side (RHS) are even numbers irrespective of the value of k, the Left Hand Side (LHS) (i.e., n2) is an odd number. Therefore, n2−1 is even.
Proof by Contradiction. A proposition p is true by contradiction if proved based on the truth of the implication ¬ p → q where q is a contradiction.
For example, to show that the sum of 2x + 1 and 2y − 1 is even, assume that the sum of 2x + 1 and 2y − 1is odd. In other words, 2(x + y), which is a multiple of 2, is odd. This is a contradiction. Hence, the sum of 2x + 1 and 2y − 1 is even.
An inference rule is a pattern establishing that if a set of premises are all true, then it can be deduced that a certain conclusion statement is true. The reference rules of addition, simplification, and conjunction need to be studied.
Proof by Induction. Proof by induction is done in two phases. First, the proposition is established to be true for a base case—typically for the positive integer 1. In the second phase, it is established that if the proposition holds for an arbitrary positive integer k, then it must also hold for the next greater integer, k + 1. In other words, proof by induction is based on the rule of inference that tells us that the truth of an infinite sequence of propositions P(n), ∀n ∈ [1 … ∞] is established if P(1) is true, and secondly, ∀k ∈ [2 ... n] if P(k) → P(k + 1).
It may be noted here that, for a proof by mathematical induction, it is not assumed that P(k) is true for all positive integers k. Proving a theorem or proposition only requires us to establish that if it is assumed P(k) is true for any arbitrary positive integer k, then P(k + 1) is also true. The correctness of mathematical induction as a valid proof technique is beyond discussion of the current text. Let us prove the following proposition using induction.
Proposition: The sum of the first n positive odd integers P(n) is n2.
Basis Step: The proposition is true for n = 1 as P(1) = 12 = 1. The basis step is complete.
Inductive Step: The induction hypothesis (IH) is that the proposition is true for n = k, k being an arbitrary positive integer k.
∴ 1 + 3 + 5+ … + (2k − 1) = k2
Now, it’s to be shown that P(k) → P(k + 1).
P(k + 1) = 1 + 3 + 5+ … +(2k − 1) + (2k + 1) = P(k) + (2k + 1) = k2 + (2k + 1) [using IH] = k2 + 2k + 1 = (k + 1)2
Thus, it is shown that if the proposition is true for n = k, then it is also true for n = k + 1.
The basis step together with the inductive step of the proof show that P(1) is true and the conditional statement P(k) → P(k + 1) is true for all positive integers k. Hence, the proposition is proved.
4 Basics of Counting
The sum rule states that if a task t1 can be done in n1 ways and a second task t2 can be done in n2 ways, and if these tasks cannot be done at the same time, then there are n1+ n2 ways to do either task.
- If A and B are disjoint sets, then |A ∪ B|=|A| + |B|.
- In general if A1, A2, …. , An are disjoint sets, then |A1 ∪ A2 ∪ … ∪ An| = |A1| + |A2| + … + |An|.
For example, if there are 200 athletes doing sprint events and 30 athletes who participate in the long jump event, then how many ways are there to pick one athlete who is either a sprinter or a long jumper? Using the sum rule, the answer would be 200 + 30 = 230.
The product rule states that if a task t1 can be done in n1 ways and a second task t2 can be done in n2 ways after the first task has been done, then there are n1 * n2 ways to do the procedure.
- If A and B are disjoint sets, then |A × B| = |A| * |B|.
- In general if A1, A2, …, An are disjoint sets, then |A1 × A2 × … × An| = |A1| * |A2| * …. * |An|.
For example, if there are 200 athletes doing sprint events and 30 athletes who participate in the long jump event, then how many ways are there to pick two athletes so that one is a sprinter and the other is a long jumper? Using the product rule, the answer would be 200 * 30 = 6000.
The principle of inclusion-exclusion states that if a task t1 can be done in n1 ways and a second task t2 can be done in n2 ways at the same time with t1, then to find the total number of ways the two tasks can be done, subtract the number of ways to do both tasks from n1 + n2.
- If A and B are not disjoint, |A ∪ B| = |A| + |B| − |A ∩ B|.
In other words, the principle of inclusionexclusion aims to ensure that the objects in the intersection of two sets are not counted more than once.
Recursion is the general term for the practice of defining an object in terms of itself. There are recursive algorithms, recursively defined functions, relations, sets, etc.
A recursive function is a function that calls itself. For example, we define f(n) = 3 * f(n − 1) for all n ∈ N and n ≠ 0 and f(0) = 5.
An algorithm is recursive if it solves a problem by reducing it to an instance of the same problem with a smaller input.
A phenomenon is said to be random if individual outcomes are uncertain but the long-term pattern of many individual outcomes is predictable.
The probability of any outcome for a random phenomenon is the proportion of times the outcome would occur in a very long series of repetitions.
The probability P(A) of any event A satisfies 0 ≤ P(A) ≤ 1. Any probability is a number between 0 and 1. If S is the sample space in a probability model, the P(S) = 1. All possible outcomes together must have probability of 1.
Two events A and B are disjoint if they have no outcomes in common and so can never occur together. If A and B are two disjoint events, P(A or B) = P(A) + P(B). This is known as the addition rule for disjoint events.
If two events have no outcomes in common, the probability that one or the other occurs is the sum of their individual probabilities.
Permutation is an arrangement of objects in which the order matters without repetition. One can choose r objects in a particular order from a total of n objects by using nPr ways, where, npr = n! / (n − r)!. Various notations like nPr and P(n, r) are used to represent the number of permutations of a set of n objects taken r at a time.
Combination is a selection of objects in which the order does not matter without repetition. This is different from a permutation because the order does not matter. If the order is only changed (and not the members) then no new combination is formed. One can choose r objects in any order from a total of n objects by using nCr ways, where, nCr = n! / [r! * (n − r)!].
5 Graphs and Trees
5.1 Graphs
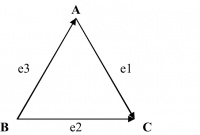
A graph G = (V, E) where V is the set of vertices (nodes) and E is the set of edges. Edges are also referred to as arcs or links.
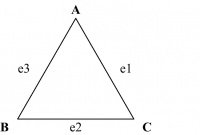
F is a function that maps the set of edges E to a set of ordered or unordered pairs of elements V. For example, in Figure 14.8, G = (V, E) where V = {A, B, C}, E = {e1, e2, e3}, and F = {(e1, (A,C)), (e2, (C, B)), (e3, (B, A))}.
The graph in Figure 14.8 is a simple graph that consists of a set of vertices or nodes and a set of edges connecting unordered pairs. The edges in simple graphs are undirected. Such graphs are also referred to as undirected graphs. For example, in Figure 14.8, (e1, (A, C)) may be replaced by (e1, (C, A)) as the pair between vertices A and C is unordered. This holds good for the other two edges too. In a multigraph, more than one edge may connect the same two vertices. Two or more connecting edges between the same pair of vertices may reflect multiple associations between the same two vertices. Such edges are called parallel or multiple edges.
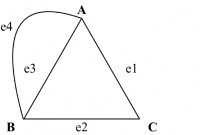
For example, in Figure 14.9, the edges e3 and e4 are both between A and B. Figure 14.9 is a multigraph where edges e3 and e4 are multiple edges.
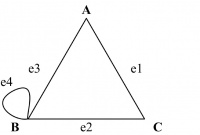
In a pseudograph, edges connecting a node to itself are allowed. Such edges are called loops.
For example, in Figure 14.10, the edge e4 both starts and ends at B. Figure 14.10 is a pseudograph in which e4 is a loop.
A directed graph G = (V, E) consists of a set of vertices V and a set of edges E that are ordered pairs of elements of V. A directed graph may contain loops.
For example, in Figure 14.11, G = (V, E) where V = {A, B, C}, E = {e1, e2, e3}, and F = {(e1, (A,C)), (e2, (B, C)), (e3, (B, A))}.
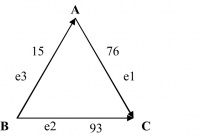
In a weighted graph G = (V, E), each edge has a weight associated with it. The weight of an edge typically represents the numeric value associated with the relationship between the corresponding two vertices.
For example, in Figure 14.12, the weights for the edges e1, e2, and e3 are taken to be 76, 93, and 15 respectively. If the vertices A, B, and C represent three cities in a state, the weights, for example, could be the distances in miles between these cities.
Let G = (V, E) be an undirected graph with edge set E. Then, for an edge e ∈ E where e = {u,v}, the following terminologies are often used:
- u, v are said to be adjacent or neighbors or connected.
- edge e is incident with vertices u and v.
- edge e connects u and v.
- vertices u and v are endpoints for edge e.
If vertex v ∈ V, the set of vertices in the undirected graph G(V, E), then:
- the degree of v, deg(v), is its number of incident edges, except that any self-loops are counted twice.
- a vertex with degree 0 is called an isolated vertex.
- a vertex of degree 1 is called a pendant vertex.
Let G(V, E) be a directed graph. If e(u, v) is an edge of G, then the following terminologies are often used:
- u is adjacent to v, and v is adjacent from u.
- e comes from u and goes to v.
- e connects u to v, or e goes from u to v.
- the initial vertex of e is u
- the terminal vertex of e is v.
If vertex v is in the set of vertices for the directed graph G(V, E), then
- in-degree of v, deg−(v), is the number of edges going to v, i.e., for which v is the terminal vertex.
- out-degree of v, deg+(v), is the number of edges coming from v, i.e., for which v is the initial vertex.
- degree of v, deg(v) = deg−(v) + deg+(v), is the sum of vs in-degree and out-degree.
- a loop at a vertex contributes 1 to both in-degree and out-degree of this vertex.
It may be noted that, following the definitions above, the degree of a node is unchanged whether we consider its edges to be directed or undirected.
In an undirected graph, a path of length n from u to v is a sequence of n adjacent edges from vertex u to vertex v.
- A path is a circuit if u=v.
- A path traverses the vertices along it.
- A path is simple if it contains no edge more than once.
A cycle on n vertices Cn for any n ≥ 3 is a simple graph where V = {v1, v2, …, vn} and E = {{v1, v2}, {v2, v3}, … , {vn−1, vn}, {vn, v1}}.
For example, Figure 14.13 illustrates two cycles of length 3 and 4.
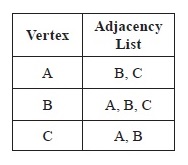
An adjacency list is a table with one row per vertex, listing its adjacent vertices. The adjacency listing for a directed graph maintains a listing of the terminal nodes for each of the vertex in the graph.
For example, Figure 14.14 illustrates the adjacency lists for the pseudograph in Figure 14.10 and the directed graph in Figure 14.11. As the out-degree of vertex C in Figure 14.11 is zero, there is no entry against C in the adjacency list.
Different representations for a graph—like adjacency matrix, incidence matrix, and adjacency lists—need to be studied.
5.2 Trees
A tree T(N, E) is a hierarchical data structure of n = |N| nodes with a specially designated root node R while the remaining n − 1 nodes form subtrees under the root node R. The number of edges |E| in a tree would always be equal to |N| − 1.
The subtree at node X is the subgraph of the tree consisting of node X and its descendants and all edges incident to those descendants. As an alternate to this recursive definition, a tree may be defined as a connected undirected graph with no simple circuits.
However, one should remember that a tree is strictly hierarchical in nature as compared to a graph, which is flat. In case of a tree, an ordered pair is built between two nodes as parent and child. Each child node in a tree is associated with only one parent node, whereas this restriction becomes meaningless for a graph where no parent-child association exists.
An undirected graph is a tree if and only if there is a unique simple path between any two of its vertices.
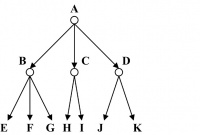
Figure 14.15 presents a tree T(N, E) where the set of nodes N = {A, B, C, D, E, F, G, H, I, J, K}. The edge set E is {(A, B), (A, C), (A, D), (B, E), (B, F), (B, G), (C, H), (C, I), (D, J), (D, K)}.
The parent of a nonroot node v is the unique node u with a directed edge from u to v. Each node in the tree has a unique parent node except the root of the tree.
For example, in Figure 14.15, root node A is the parent node for nodes B, C, and D. Similarly, B is the parent of E, F, G, and so on. The root node A does not have any parent.
A node that has children is called an internal node. For example, in Figure 14.15, node A or node B are examples of internal nodes. The degree of a node in a tree is the same as its number of children. For example, in Figure 14.15, root node A and its child B are both of degree 3. Nodes C and D have degree 2.
The distance of a node from the root node in terms of number of hops is called its level. Nodes in a tree are at different levels. The root node is at level 0. Alternately, the level of a node X is the length of the unique path from the root of the tree to node X.
For example, root node A is at level 0 in Figure 14.15. Nodes B, C, and D are at level 1. The remaining nodes in Figure 14.15 are all at level 2. The height of a tree is the maximum of the levels of nodes in the tree. For example, in Figure 14.15, the height of the tree is 2.
A node is called a leaf if it has no children. The degree of a leaf node is 0. For example, in Figure 14.15, nodes E through K are all leaf nodes with degree 0. The ancestors or predecessors of a nonroot node X are all the nodes in the path from root to node X. For example, in Figure 14.15, nodes A and D form the set of ancestors for J.
The successors or descendents of a node X are all the nodes that have X as its ancestor. For a tree with n nodes, all the remaining n − 1 nodes are successors of the root node. For example, in Figure 14.15, node B has successors in E, F, and G. If node X is an ancestor of node Y, then node Y is a successor of X.
Two or more nodes sharing the same parent node are called sibling nodes. For example, in Figure 14.15, nodes E and G are siblings. However, nodes E and J, though from the same level, are not sibling nodes. Two sibling nodes are of the same level, but two nodes in the same level are not necessarily siblings.
A tree is called an ordered tree if the relative position of occurrences of children nodes is significant. For example, a family tree is an ordered tree if, as a rule, the name of an elder sibling appears always before (i.e., on the left of) the younger sibling.
In an unordered tree, the relative position of occurrences between the siblings does not bear any significance and may be altered arbitrarily.
A binary tree is formed with zero or more nodes where there is a root node R and all the remaining nodes form a pair of ordered subtrees under the root node.
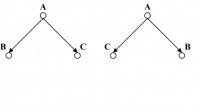
In a binary tree, no internal node can have more than two children. However, one must consider that besides this criterion in terms of the degree of internal nodes, a binary tree is always ordered. If the positions of the left and right subtrees for any node in the tree are swapped, then a new tree is derived. For example, in Figure 14.16, the two binary trees are different as the positions of occurrences of the children of A are different in the two trees.
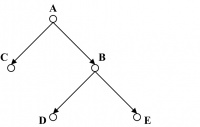
According to [1*], a binary tree is called a full binary tree if every internal node has exactly two children. For example, the binary tree in Figure 14.17 is a full binary tree, as both of the two internal nodes A and B are of degree 2. A full binary tree following the definition above is also referred to as a strictly binary tree.
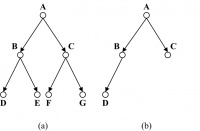
For example, both binary trees in Figure 14.18 are complete binary trees. The tree in Figure 14.18(a) is a complete as well as a full binary tree. A complete binary tree has all its levels, except possibly the last one, filled up to capacity. In case the last level of a complete binary tree is not full, nodes occur from the leftmost positions available.
Interestingly, following the definitions above, the tree in Figure 14.18(b) is a complete but not full binary tree as node B has only one child in D. On the contrary, the tree in Figure 14.17 is a full —but not complete—binary tree, as the children of B occur in the tree while the children of C do not appear in the last level. A binary tree of height H is balanced if all its leaf nodes occur at levels H or H − 1. For example, all three binary trees in Figures 14.17 and 14.18 are balanced binary trees.
There are at most 2H leaves in a binary tree of height H. In other words, if a binary tree with L leaves is full and balanced, then its height is H = ⌈log2L⌉.
For example, this statement is true for the two trees in Figures 14.17 and 14.18(a) as both trees are full and balanced. However, the expression above does not match for the tree in Figure 14.18(b) as it is not a full binary tree.
A binary search tree (BST) is a special kind of binary tree in which each node contains a distinct key value, and the key value of each node in the tree is less than every key value in its right subtree and greater than every key value in its left subtree.
A traversal algorithm is a procedure for systematically visiting every node of a binary tree. Tree traversals may be defined recursively.
If T is binary tree with root R and the remaining nodes form an ordered pair of nonnull left subtree TL and nonnull right subtree TR below R, then the preorder traversal function PreOrder(T) is defined as:
PreOrder(T) = R, PreOrder(TL), PreOrder(TR) … eqn. 1
The recursive process of finding the preorder traversal of the subtrees continues till the subtrees are found to be Null. Here, commas have been used as delimiters for the sake of improved readability.
The postorder and in-order may be similarly defined using eqn. 2 and eqn. 3 respectively.
PostOrder(T) = PostOrder(TL), PostOrder(TR), R … eqn 2
InOrder(T) = InOrder(TL), R, InOrder(TR) …eqn 3
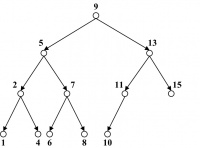
For example, the tree in Figure 14.19 is a binary search tree (BST). The preorder, postorder, and in-order traversal outputs for the BST are given below in their respective order.
Preorder output: 9, 5, 2, 1, 4, 7, 6, 8, 13, 11, 10, 15
Postorder output: 1, 4, 2, 6, 8, 7, 5, 10, 11, 15, 13, 9
In-order output: 1, 2, 4, 5, 6, 7, 8, 9, 10, 11, 13, 15
Further discussion on trees and their usage has been included in section 6, Data Structure and Representation, of the Computing Foundations KA.
6 Discrete Probability
Probability is the mathematical description of randomness. Basic definition of probability and randomness has been defined in section 4 of this KA. Here, let us start with the concepts behind probability distribution and discrete probability.
A probability model is a mathematical description of a random phenomenon consisting of two parts: a sample space S and a way of assigning probabilities to events. The sample space defines the set of all possible outcomes, whereas an event is a subset of a sample space representing a possible outcome or a set of outcomes.
A random variable is a function or rule that assigns a number to each outcome. Basically, it is just a symbol that represents the outcome of an experiment.
For example, let X be the number of heads when the experiment is flipping a coin n times. Similarly, let S be the speed of a car as registered on a radar detector.
The values for a random variable could be discrete or continuous depending on the experiment. A discrete random variable can hold all possible outcomes without missing any, although it might take an infinite amount of time. A continuous random variable is used to measure an uncountable number of values even if an infinite amount of time is given.
For example, if a random variable X represents an outcome that is a real number between 1 and 100, then X may have an infinite number of values. One can never list all possible outcomes for X even if an infinite amount of time is allowed. Here, X is a continuous random variable. On the contrary, for the same interval of 1 to 100, another random variable Y can be used to list all the integer values in the range. Here, Y is a discrete random variable.
An upper-case letter, say X, will represent the name of the random variable. Its lower-case counterpart, x, will represent the value of the random variable.
The probability that the random variable X will equal x is:
P(X = x) or, more simply, P(x).
A probability distribution (density) function is a table, formula, or graph that describes the values of a random variable and the probability associated with these values.
Probabilities associated with discrete random variables have the following properties:
i. 0 ≤ P(x) ≤ 1 for all x
ii. ΣP(x) = 1
A discrete probability distribution can be represented as a discrete random variable.
The mean μ of a probability distribution model is the sum of the product terms for individual events and its outcome probability. In other words, for the possible outcomes x1, x2, … , xn in a sample space S if pk is the probability of outcome xk, the mean of this probability would be μ = x1p1 + x2p2 + … + xnpn.
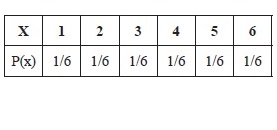
For example, the mean of the probability density for the distribution in Figure 14.20 would be
1 * (1/6) + 2 * (1/6) + 3 * (1/6) + 4 * (1/6) + 5 * (1/6) + 6 * (1/6) = 21 * (1/6) = 3.5
Here, the sample space refers to the set of all possible outcomes.
The variance s2 of a discrete probability model is: s2 = (x1 – μ)2p1 + (x2 – μ)2p2 + … + (xk – μ)2pk.
The standard deviations is the square root of the variance.
For example, for the probability distribution in Figure 14.20, the variation σ2 would be
s2 = [(1 – 3.5)2 * (1/6) + (2 – 3.5)2 * (1/6) + (3 – 3.5)2 * (1/6) + (4 – 3.5)2 * (1/6) + (5 – 3.5)2 * (1/6) + (6 – 3.5)2 * (1/6)] = (6.25 + 2.25 + 0.25 + 0.5 + 2.25 + 6.25) * (1/6) = 17.5 * (1/6) = 2.90
∴ standard deviation s =
These numbers indeed aim to derive the average value from repeated experiments. This is based on the single most important phenomenon of probability, i.e., the average value from repeated experiments is likely to be close to the expected value of one experiment. Moreover, the average value is more likely to be closer to the expected value of any one experiment as the number of experiments increases.
7 Finite State Machines
A computer system may be abstracted as a mapping from state to state driven by inputs. In other words, a system may be considered as a transition function T: S × I → S × O, where S is the set of states and I, O are the input and output functions. If the state set S is finite (not infinite), the system is called a finite state machine (FSM).
Alternately, a finite state machine (FSM) is a mathematical abstraction composed of a finite number of states and transitions between those states. If the domain S × I is reasonably small, then one can specify T explicitly using diagrams similar to a flow graph to illustrate the way logic flows for different inputs. However, this is practical only for machines that have a very small information capacity.
An FSM has a finite internal memory, an input feature that reads symbols in a sequence and one at a time, and an output feature.
The operation of an FSM begins from a start state, goes through transitions depending on input to different states, and can end in any valid state. However, only a few of all the states mark a successful flow of operation. These are called accept states.
The information capacity of an FSM is C = log |S|. Thus, if we represent a machine having an information capacity of C bits as an FSM, then its state transition graph will have |S| = 2C nodes.
A finite state machine is formally defined as M = (S, I, O, f, g, s0).
S is the state set; I is the set of input symbols; O is the set of output symbols; f is the state transition function; g is the output function; and s0 is the initial state.
Given an input x ∈ I on state Sk, the FSM makes a transition to state Sh following state transition function f and produces an output y ∈ O using the output function g.
For example, Figure 14.21 illustrates an FSM with S0 as the start state and S1 as the final state. Here, S = {S0, S1, S2}; I = {0, 1}; O = {2, 3}; f(S0, 0) = S2, f(S0, 1) = S1, f(S1, 0) = S2, f(S1, 1) = S2, f(S2, 0) = S2, f(S2, 1) = S0; g(S0, 0) = 3, g(S0, 1) = 2, g(S1, 0) = 3, g(S1, 1) = 2, g(S2, 0) = 2, g(S2, 1) = 3.